You can download the calculator on my other post here
I also explain the math for distance to horizon and line of sight here.
I have found a few different methods that are pretty accurate up to around 100 miles. Then there is a more complex method that is accurate up to 3,963 miles which is the radius of the earth. So dust off your old geometry and trig books and let's begin!
Zetetic Astronomy
So the first method I need to mention is from Samuel Birley Rowbotham. He is mentioned frequently by the Flat Earth Society and his math is used in many flat earth videos. He believed the Earth was flat and published a book recording his experiments called Zetetic Astronomy, Earth Not a Globe. You can check it out here.
Rowbotham states that if the earth is 25,000 miles in circumference then the curvature would be 8 inches per mile.
Pythagorean Theorem
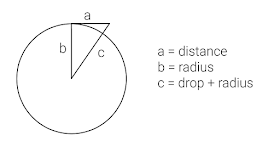
The next method uses the Pythagorean Theorem which says that the sum of the square of adjacent and opposite sides equals the square of the hypotenuse in a right triangle. a² + b² = c².
So we are trying to find the distance the Earth drops down per mile. So the equation would be radius² + distance² = (radius + drop)². If we are trying to find the drop we can change the equation to
√(r² + d²)
- r = drop.
Putting that into a calculator you get drop = .000126 mi. There are 5280 feet in a mile and 12 inches in a foot. So .000126 * 5280 * 12 = 7.98336 in.
Trigonometry
I might have to apologize to my math teacher for telling her I would never use this information. The next method is the hardest so I'm going to try my best to explain. The next method uses SIN COS and TAN. If you need a way better way of explaining it then go here.
So if you don't remember, to solve this we use SOH CAH TOA.
Sine = Opposite / Hypotenuse
Cosine = Adjacent / Hypotenuse
Tangent = Opposite / Adjacent
Using this information we can solve the curvature like this
In this example r = radius, d = distance, h = height/drop, L = length, and a = angle. Based off of this we know we find the height by subtracting the length of the triangle from the radius. How do we find that? back to the math!
We need to find the angle of a by using SIN(a) = d/r. Using the inverse of sine gives us the angle a = Sin-1(d/r). Using that we can use COS(a) = L/r changed to find L is COS(a) * r = L. Then we take L and subtract from the radius. Still with me?
The full equation is [r - (COS(SIN-1(d/r)) * r) = L] so let's plug that in. [3963 - ((COS(SIN-1(1/3963))) * 3963)]. If I typed this correctly it comes out to .000126168. Multiply that by 5280 and 12 we get 7.994 inches! We did it!
I apologize if any of that was confusing, I tried my best!




ReplyDeleteThe curvature formula presented by the flat earthers CANNOT be right.
WIDTH has ZERO effect on how curved or not curved the earth is over any given distance.
If you don't believe me check it out yourself, using an orange or a ball and a tape measure, the amount of curvature does not increase when you measure a longer distance!
They are applying the square to the wrong element of the formula, the distance!
How does that make any sense? In other words, the curvature of 1 mile would be; 1 mile x 1 mile x 8 inches = 8 inches, while a 2 mile curvature = 2 miles x 2 miles x 8 inches = 32 inches?! Obviously that's not right, it can't be both!
It SHOULD be applied to the HEIGHT of the observer, in order to determine the curvature of the earth using the Pythagorean theorem, but since that's been done, we know the curvature of the earth is 8 inches per mile.
Get your calculator on your phone out, and you can see how nonsensical that formula gets, if you increase the numbers;
3x3x8=72
4x4x8=128
5x5x8=200
6x6x8=288
you can see it doesn't even follow a logical progression- it gets larger by a little more each time you try and figure out what the curvature is depending on what distance you use(?!wtf) , the result is that the earth's curvature is constantly changing?!
or in other words, the curvature or drop off of the earth over one mile is 8 inches but over 6 miles it's 24 feet(36 times greater than at 1 mile!?)? Obviously these both cannot be true.
So here I've shown using simple math that the curvature formula presented by the flat earthers CANNOT be right.
The 8 inches per mile squared is actually correct for up to around 100 miles. If you draw a large circle and a straight edge extending straight out from the top of the circle, you will see that each incremental measuring unit along the straight edge correlates with a longer drop than did the previous unit.
DeleteThat's because you're describing a Ball with math. This calc has been around a very long time. It dates back to Pythagoras, I believe. This is Geometry. I am no mathematician but I can tell, neither are you.
DeleteFirst of all, you're confusing drop with curvature, secondly, all you need to do is use you eyes. When you look at a mountain range that is 50 miles away and it is still perpendicular to the plane you are on, that proves there is NO DROP! On a ball earth, if those mountains were visible, they would NOT be perpendicular, they would be leaning way and you could NOT see their peaks!
DeletePatently absurd answer. The commenter claims they can tell if mountains are "leaning away" just 50 miles away. That idea is preposterous at best, since in 50 miles, the Earth curves less than a degree! You can't even tell if a vertical surface that is exactly plumb is "leaning away" at 50 miles, UNLESS, and this is the good part, you use a theodolite. This is second nature to surveyors who do exactly this every day, falsifying the premise. You CAN tell if something is leaning away from you, and it doesn't have to be 50 miles out, as long as you you as accurate instrument to measure the angle.
Deletethe 8 inches per mile squared formula is not correct for getting the curve of the earth. That formula is for calculating a parabola, not the curve of a sphere.
ReplyDeleteThat is correct. Please see my youtube channel about all this. https://www.youtube.com/channel/UCZLv2K1MKflsdjotirpfqjg?view_as=subscriber
DeleteSteve Walden-right on saw that mistake top down theres the illumanti mock
DeleteIt works perfectly fine for hundreds of miles, which is all that is required in this context. People who say it doesn't work BECAUSE it is a parabola don't know what they're talking about. It does work with a very reasonable degree of accuracy, even if it is parabolic, for distance of a few hundred miles or less, in this context. There is an error, but it's not nearly as bad as this comment makes out.
DeleteDrop is not curvature. You make the the mistake of confusing the two.
ReplyDeleteLol...why are you attributing this calculation to so called Flat Earthers? This was the official calculations of main stream science until Flat Earthers called bullshit on it and now science is projecting their folly on someone else.
ReplyDeleteNo, it never has and NEVER will be how you calculate the curve of a circle. Your blatant misunderstanding of a parabola and a circle is entirely your own fault.
DeleteActually, it is the accepted method for estimating DROP for a few hundred miles, and was derived mathematically by surveyors by ignoring inconsequential terms where distances d are much smaller than R.
DeleteMiles squared, times 8" works, but at some point, you need a another formula when the arc exceeds 90 degrees. This is computed using pi, which calls for even more drop than the 8" that the ball earthers are already tormented by.
ReplyDeleteI believe the number gets greater the further you go, you have remember at the total of feet around is a circle the miles dropped would be tremendous.
ReplyDeleteThe real life formula for the Earth's surface curvature is one degree per 69 miles or 111 km.
ReplyDeleteThe "eight inches per (mile squared)" formula diverges from reality after several miles, because it describes a parabola, not a circle. Rowbotham knew Flat Earth is a pack of lies. He was a scammer. He started Flat Earth because his quack cures business wasn't doing well.