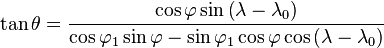Azimuthal Equidistant Calculator

You can download the calculator by clicking the link here: Download

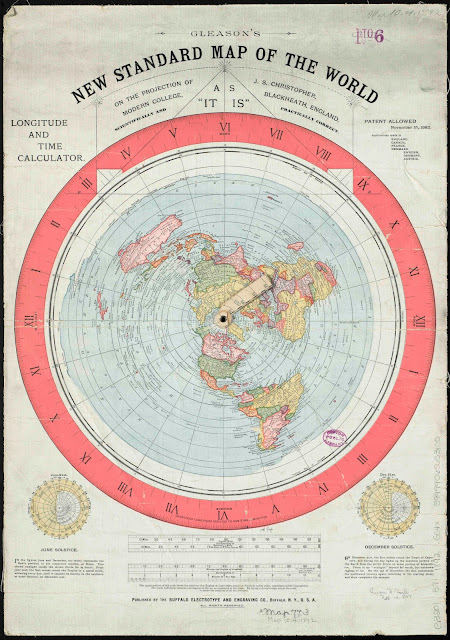
Because the Azimuthal Equidistant Projection is used so frequently by Flat Earth Theorists I really wanted to learn how it works. The map definition from Wikipedia is this:

A point on the globe is chosen to be special in the sense that mapped distances and azimuths from that point to any other point will be correct. That point, (φ₁, λ₀), will project to the center of a circular projection, with φ referring to latitude and λ referring to longitude. All points along a given azimuth will project along a straight line from the center, and the angle θ that line subtends from the vertical is the azimuth angle. The distance from the center point to another projected point is given as ρ. By this description, then, the point on the globe specified by (θ,ρ) will be projected to Cartesian coordinates:

The relationship between the coordinates (θ,ρ) of the point on the globe, and its latitude and longitude coordinates (φ, λ) is found as follows. The great circle distance ρ between two points (φ₁, λ₀) and (φ, λ) on the sphere is given by:

The azimuth from the first to the second point is given by:

When the center point is the north pole, these formulas greatly simplify to:

At first glance it was very overwhelming and confusing but It helped to create a calculator. First you need to pick a center point, for Gleason's map it's the North Pole. From there you can calculate the distance to any given point and the Azimuth angle. These can then be turned into Cartesian coordinates where the spot on the globe will be projected on the map.

After a lot of trial and error I managed to get the coordinates correct. First thing is to not use the longitude on the map but rather have 0 degrees begin at the bottom. From there you go a full 360 degrees in a counter-clockwise direction. So moving to the right from zero would be 15, 30, 45, 60, 75, 90, 105, etc...The latitude on the map is correct but when you input degrees after the equator make it negative. So moving away from the center point would be 75, 60, 45, 30, 15, 0, -15, -30, etc...

Now let's test it. I would like to plot this line:

In my example I use 105 degree longitude and start from the center point and move outward. I then plot (in Radians) the x and y in Cartesian Coordinates.

I've tested several and they all seem to plot out like they do on the map. If you would like to test it yourself, you can use the interactive one I used on tutor.com.

Also I would like to mention that to calculate distance both points need to be along the same line of longitude. The map only projects distances accurately from the center point. In the calculator it will show the distance in degrees from the center point. According to Gleason's map you multiply degrees by 60 to calculate the distance in miles. So if the size between two points on the same line of latitude is 45 degrees it would calculate to 60 miles x 45 degrees = 2700 miles on Gleason's map. 

Thank you for reading and I hope everything made sense. Please feel free to point out and correct any mistakes I've made. I would like this to be accurate. Please don't hesitate to offer criticisms, suggestions, questions, future topics, or if you just want to have a conversation in the comments.

The Flat Earth Map

I wanted to learn more about the flat earth map. From what I've read and seen so far most Flat Earthers refer to a specific map as the most realistic projection of Earth. This map is specifically called an

Azimuthal Equidistant Projection

This projection displays all points at proportionately correct distances from the center point. Points that are not along a single point of longitude become more distorted the farther they are from the center point. This type of projection is useful for airplane paths and radio transmitters.

Gleason's 1892 World Map

The map that seems to be referred to as the most accurate is the Gleason's New Standard Map of the World. At first glance it is very detailed with latitude, longitude, and time zones. The center point of the map is the North Pole and Antarctica surrounds the outside.

You can download the full resolution map by clicking the link: Download

The next step is to analyze the scale of the map. The maps scale displays English miles corresponding to nautical miles. Nautical miles referring to miles over seas. My first question was why it was not a constant scale if it was a true representation of Earth. But I'm not entirely sure so let's check out the math on the projection.

I created a calculator and explain the math on my next post here.