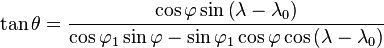I Finally Launched My YouTube Channel!

I love discussing Flat Earth and I finally started my YouTube series! Since I really enjoy learning and researching new things I thought this would be fun to interact with the community and work together to find the best evidence proving whether the Earth is a flat plane or a ball planet! I know it's easier said than done, but no matter which model is correct, I hope we can find good enough evidence to convince even the most stubborn person.

Knowing the internet can be a mean place I was very nervous posting my first video, but I was pleasantly surprised when everyone was really nice and supportive! I spent a month researching and another month figuring out the best way to display both Earth models on screen. After a lot of trial and error I finally put together my first video. Talking into a microphone instead of another person is a lot harder than I thought it would be. Hopefully I'll get better quickly haha.

For my first video I decided to tackle some of the most popular topics about the horizon. In this video I look at the flat horizon line, our eye level, objects beyond the horizon, and analyze Jeranism's laser test. I also create a 3D mockup of Flat Earth and a to scale illustration of Round Earth.

I finally posted my second video! I was hoping to have it done sooner but these videos take a lot of work but hopefully I can get in a good rhythm and get videos out faster. I just don't want to rush it because I want to make sure my research and analysis is accurate.

In my second video I tackle questions from the comments on my first video. I look at the math involved with the Earth being an oblate spheroid, ships on the horizon, and high altitude balloon footage. I also analyze specific examples from the comments. First is O'ahu visible from Kauai and the other is Corsica to Isola d’Elba.

Azimuthal Equidistant Calculator

You can download the calculator by clicking the link here: Download

Because the Azimuthal Equidistant Projection is used so frequently by Flat Earth Theorists I really wanted to learn how it works. The map definition from Wikipedia is this:

A point on the globe is chosen to be special in the sense that mapped distances and azimuths from that point to any other point will be correct. That point, (φ₁, λ₀), will project to the center of a circular projection, with φ referring to latitude and λ referring to longitude. All points along a given azimuth will project along a straight line from the center, and the angle θ that line subtends from the vertical is the azimuth angle. The distance from the center point to another projected point is given as ρ. By this description, then, the point on the globe specified by (θ,ρ) will be projected to Cartesian coordinates:

The relationship between the coordinates (θ,ρ) of the point on the globe, and its latitude and longitude coordinates (φ, λ) is found as follows. The great circle distance ρ between two points (φ₁, λ₀) and (φ, λ) on the sphere is given by:

The azimuth from the first to the second point is given by:

When the center point is the north pole, these formulas greatly simplify to:

At first glance it was very overwhelming and confusing but It helped to create a calculator. First you need to pick a center point, for Gleason's map it's the North Pole. From there you can calculate the distance to any given point and the Azimuth angle. These can then be turned into Cartesian coordinates where the spot on the globe will be projected on the map.

After a lot of trial and error I managed to get the coordinates correct. First thing is to not use the longitude on the map but rather have 0 degrees begin at the bottom. From there you go a full 360 degrees in a counter-clockwise direction. So moving to the right from zero would be 15, 30, 45, 60, 75, 90, 105, etc...The latitude on the map is correct but when you input degrees after the equator make it negative. So moving away from the center point would be 75, 60, 45, 30, 15, 0, -15, -30, etc...

Now let's test it. I would like to plot this line:

In my example I use 105 degree longitude and start from the center point and move outward. I then plot (in Radians) the x and y in Cartesian Coordinates.

I've tested several and they all seem to plot out like they do on the map. If you would like to test it yourself, you can use the interactive one I used on tutor.com.

Also I would like to mention that to calculate distance both points need to be along the same line of longitude. The map only projects distances accurately from the center point. In the calculator it will show the distance in degrees from the center point. According to Gleason's map you multiply degrees by 60 to calculate the distance in miles. So if the size between two points on the same line of latitude is 45 degrees it would calculate to 60 miles x 45 degrees = 2700 miles on Gleason's map. 

Thank you for reading and I hope everything made sense. Please feel free to point out and correct any mistakes I've made. I would like this to be accurate. Please don't hesitate to offer criticisms, suggestions, questions, future topics, or if you just want to have a conversation in the comments.

The Flat Earth Map

I wanted to learn more about the flat earth map. From what I've read and seen so far most Flat Earthers refer to a specific map as the most realistic projection of Earth. This map is specifically called an

Azimuthal Equidistant Projection

This projection displays all points at proportionately correct distances from the center point. Points that are not along a single point of longitude become more distorted the farther they are from the center point. This type of projection is useful for airplane paths and radio transmitters.

Gleason's 1892 World Map

The map that seems to be referred to as the most accurate is the Gleason's New Standard Map of the World. At first glance it is very detailed with latitude, longitude, and time zones. The center point of the map is the North Pole and Antarctica surrounds the outside.

You can download the full resolution map by clicking the link: Download

The next step is to analyze the scale of the map. The maps scale displays English miles corresponding to nautical miles. Nautical miles referring to miles over seas. My first question was why it was not a constant scale if it was a true representation of Earth. But I'm not entirely sure so let's check out the math on the projection.

I created a calculator and explain the math on my next post here.

How to Calculate Distance to Horizon and Line of Sight

My first couple of questions after calculating curvature was well how far can I see? and how far does a building or object have to be before I can't see it anymore? So we need to figure out where the horizon is. More math! Yay!

You can download the calculator I made on my other post here.

Calculating Distance to Horizon

To calculate this we use the Pythagorean Theorem again but just solving for the distance instead of height. If you want the height equation click here.

So we start with this

If a² + b² = c² then for this example we get radius² + distance² = (height + radius)². So to solve for distance we just subtract radius from both sides and square the whole thing. Then we get distance = √(r + h)² - r².

If we fill in the numbers we get distance = √(3963 + .001136)² - 3963²   (To get miles we divide 6 feet by 5280 which equals .001136). This then becomes distance = √9.00393 = 3.00. So a person with their eye level at 6 feet will see the horizon at 3 miles.

If you wanted to use an approx. method just use 1.22 *√h.

Line of Sight

So now we can use the same equation to find out how far away we can see an object. First you add the distance to horizon for each height together.  So if there are 2 people with an eye level of 6 feet we know they can each see 3 miles. 3 + 3 = 6. So this means they can see each other at a Maximum of 6 miles.

So if we know how far any height can be from the horizon we can determine how much is visible over the curve of the earth. We can take the Maximum distance and subtract the distance from object 1 to object 2. Then use the equation √(r² + d²) - r = h or approximate formula h = (d/1.22)².

So let's try an example. If a person has an eye level of 6 feet and they are viewing a building 6 miles away. The building is 30 feet tall. We know a 6 foot eye level can see 3 miles to the horizon. Then we calculate and distance for a 30 foot building to be 6.7 miles. So the total possible distance for a person to see the tip of the building is 9.7 miles. Then subtract the distance between the person and the object. 9.7 - 6 = 3.7 miles. 

Now we can plug that in. √(3963² + 3.7²) - 3963² =  .001727. Multiply that by 5280 we get 9.12 feet. Using the approx. method (3.7/1.22)² = 9.2 feet.  Using either method we find that about 9 feet of the building is hidden below the horizon.

If you need to account for refraction there is an approximate method for that as well. Instead of 1.22 use 1.32. So the approximate refraction formula would be h = (d/1.32)².

If I didn't explain it well enough, Wikipedia does a great job here. 

Please do not hesitate to let me know if I made any mistakes. I would like all the information to be correct so any feedback is appreciated! Thank you!

How to Calculate Earth's Curvature

There are a few different definitions of curvature and several ways to calculate it. See curvature on Wikipedia.
You can download the calculator on my other post here
I also explain the math for distance to horizon and line of sight here.

I have found a few different methods that are pretty accurate up to around 100 miles. Then there is a more complex method that is accurate up to 3,963 miles which is the radius of the earth. So dust off your old geometry and trig books and let's begin!

Zetetic Astronomy

So the first method I need to mention is from Samuel Birley Rowbotham. He is mentioned frequently by the Flat Earth Society and his math is used in many flat earth videos. He believed the Earth was flat and published a book recording his experiments called Zetetic Astronomy, Earth Not a Globe. You can check it out here.

Rowbotham states that if the earth is 25,000 miles in circumference then the curvature would be 8 inches per mile.

To use his calculation you just square the mileage and multiply by 8. So if you use 3 miles it is 3 squared (9) and multiply by 8 (72), which is 6 feet. Therefore the Earth drops 6 feet in 3 miles.

Pythagorean Theorem

The next method uses the Pythagorean Theorem which says that the sum of the square of adjacent and opposite sides equals the square of the hypotenuse in a right triangle. a² + b² = c².

So we are trying to find the distance the Earth drops down per mile. So the equation would be radius² + distance² = (radius + drop)². If we are trying to find the drop we can change the equation to √(r² + d²) - r = drop.

If the radius is 3,963 miles and the distance is 1 mile we can solve the equation. √(3963² + 1²) - 3963 = drop.

Putting that into a calculator you get drop = .000126 mi. There are 5280 feet in a mile and 12 inches in a foot. So .000126 * 5280 * 12 = 7.98336 in.

Trigonometry

I might have to apologize to my math teacher for telling her I would never use this information. The next method is the hardest so I'm going to try my best to explain. The next method uses SIN COS and TAN. If you need a way better way of explaining it then go here.

So if you don't remember, to solve this we use SOH CAH TOA.

Sine = Opposite / Hypotenuse
Cosine = Adjacent / Hypotenuse
Tangent = Opposite / Adjacent

Using this information we can solve the curvature like this

In this example r = radius, d = distance, h = height/drop,  L = length, and a = angle. Based off of this we know we find the height by subtracting the length of the triangle from the radius.  How do we find that? back to the math!

We need to find the angle of a by using SIN(a) = d/r. Using the inverse of sine gives us the angle a = Sin-1(d/r). Using that we can use COS(a) = L/r changed to find L is COS(a) * r = L. Then we take L and subtract from the radius. Still with me?

The full equation is [r - (COS(SIN-1(d/r)) * r) = L] so let's plug that in. [3963 - ((COS(SIN-1(1/3963))) * 3963)]. If I typed this correctly it comes out to .000126168. Multiply that by 5280 and 12 we get 7.994 inches! We did it! 

I apologize if any of that was confusing, I tried my best!

Earth Curvature Calculator

The calculator includes 3 different formulas for curvature and 3 for line of sight.
You can download the calculator by clicking the link here: Download

How To Use The Calculator

Only enter numbers in the yellow boxes

The first step is to input Earth's circumference (in miles). The entire calculator refers to these numbers. So if you input earth's circumference to be 50,000 miles then the curvature and line of sight equations will change according to that.

I also included a conversion calculator. Use the yellow boxes to input miles, feet, inches, or kilometers.

The next step is to input the distance for curvature. So if you input 1 mile it will change the rest of the equations to 1 mile. In the example you can see that the curvature is 8 inches for 1 mile using the Zetetic equation and 7.99 inches using the Pythagorean Theorem and Trigonometry Formula. All equations (besides Zetetic) are affected by the dimensions of the earth above.

The last part of the calculator is line of sight. Input an eye level and height of an object (in feet) and it will calculate the distance to the horizon for each height. (input height above sea level to be exact)

This will calculate the maximum distance you can be from the object before it disappears under the horizon. If you know the distance to the object it will calculate how much of the object is visible above the horizon and how much is hidden below it. So in the example, if your eye level is at 6 feet above sea level and you are 6 miles away from a 10 foot object above sea level then 4 Feet of the object is visible while 6 feet is hidden below the horizon.

It is important to include sea level in your calculation. If you are viewing a 80 foot building and it begins at 20 feet above sea level than use a height of 100 feet. Also be aware the amount that is calculated for visible and hidden considers the whole height as one object. (Example: If the amount visible for the total 100 foot height is 40 feet then you should only be seeing half of the 80 foot building).

I also included an approximate refraction formula if anyone needs it. I got the formula from this Wikipedia article.

If you would like to know more about the equations I use I explain it in my post here

Well that's it! Please feel free to point out and correct any mistakes I have made. That is how we all learn and I want this to be as useful as possible. Don't hesitate to let me know if you have any criticisms, questions, and/or suggestions. I hope this helps as you research, hypothesize, theorize, test and analyze! Thanks for reading!